“Metron Ariston”  pendant

The Art of Balance

In a world full of excess and deficiency, the search for the Middle Way is an attitude. The “Metron Ariston” is not just any ancient saying, but the quintessential essence of Greek philosophy. Attributed to Cleobulus, one of the Seven Sages of antiquity, it’s the formulation of the recipe for the best possible outcome of every action.

The concept of Metron is not a midpoint or a mathematical average, but an undefined, fluid boundary between two extremes. It is what is fitting, the Ariston (the perfect) for each circumstance. Finding it requires a critical vigilance that leads to a clear overview of reality and harmony with ourselves and others.

A Philosophical Jewelry for Your Personal Metron

The “Metron Ariston” pendant is your companion in the daily search for optimal decisions. By wearing it, you strengthen your belief that you have the freedom and the responsibility for the personal choice on the path to your evolution. It is a piece of jewelry with a strong meaning that inspires you to avoid “hubris” – the violations of the Order of the Cosmos – and to find the ideal measure in every step you take. It will help you bring beauty and balance into your life.

Because finding Metron is the art of the ideal choice for a given space and time in every field of thought; and that is truly magical.

Script & Geometry

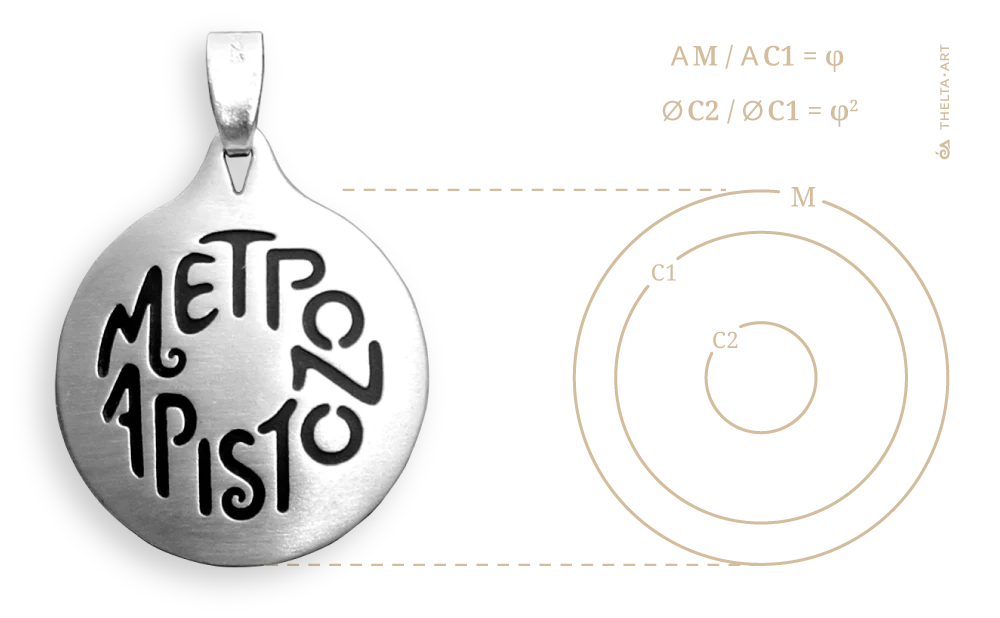
The motif design brings out the wide meaning range of the concept of “mėtron”, enclosing the glyphs into a ring that adheres to the most appropriate mathematical ratio that expresses it: the Golden ratio.

Specifically, the area of the circle defined by the jewel compared to the area of the outer circle of the ring that encloses the writing have a golden ratio relation. Therefore, it is: AM / AC = φ (1.618)

Additionally, the ratio of the diameter of the larger circle of the ring to the smaller one is the golden ratio… squared! Therefore, it is: ØC1 / ØC2 = φ² (2.618)